Trang blog của Nguyễn Thế Dũng - ĐHSP Huế. Mời đọc.
Học máy theo cách tiếp cận thống kê và minh hoạ với Python
Đây là tài liệu được lược dịch và chuyển soạn từ: https://www.statology.org/machine-learning-tutorials/ để bà con dễ học.
---------------------------------------
Bài 1. Sơ lược về học có giám sát và không giám sát
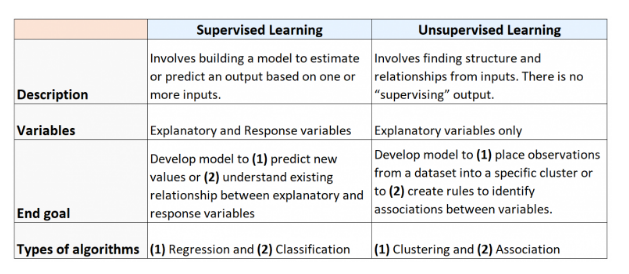
Lĩnh vực học máy bao gồm rất nhiều thuật toán được sử dụng để khai phá dữ liệu. Các thuật toán này có thể được phân loại thành một trong hai loại:
1. Thuật toán học có giám sát: Liên quan đến việc xây dựng một mô hình để ước tính hoặc dự đoán kết quả đầu ra dựa trên một hoặc nhiều đầu vào.
2. Thuật toán học không giám sát: Liên quan đến việc tìm kiếm cấu trúc và mối quan hệ từ các đầu vào. Không có đầu ra "giám sát".
Thuật toán học có giám sát
Một thuật toán hhojc có giám sát được sử dụng khi chúng ta có một hoặc nhiều biến giải thích (X1 , X2 , X3 , ..., X p ) và một biến phản ứng (Y) và chúng ta muốn tìm một số chức năng mô tả mối quan hệ giữa biến giải thích và biến phản hồi:
Y = f (X) + ε
trong đó f đại diện cho thông tin có hệ thống mà X cung cấp về Y và trong đó ε là thuật ngữ sai số ngẫu nhiên độc lập với X với giá trị trung bình bằng 0.
Có hai loại thuật toán học có giám sát chính:
1. Hồi quy: Biến đầu ra là liên tục (ví dụ: cân nặng, chiều cao, thời gian, v.v.)
2. Phân loại: Biến đầu ra có tính phân loại (ví dụ: nam hay nữ, đạt hay không đạt, hiền hay không hiền lành, v.v.)
Có hai lý do chính mà chúng ta sử dụng thuật toán học có giám sát:
1. Dự đoán: Chúng ta thường sử dụng một tập hợp các biến giải thích để dự đoán giá trị của một số biến phản hồi (ví dụ: sử dụng diện tích vuông và số lượng phòng ngủ để dự đoán giá nhà )
2. Suy luận: Chúng ta có thể quan tâm đến cách mà một biến phản ứng bị ảnh hưởng khi giá trị của các biến giải thích thay đổi (ví dụ: giá nhà trung bình tăng bao nhiêu khi số phòng ngủ tăng một?)
Tùy thuộc vào mục tiêu của chúng ta là suy luận hay dự đoán (hoặc kết hợp cả hai), chúng ta có thể sử dụng các phương pháp khác nhau để ước lượng hàm f. Ví dụ: các mô hình tuyến tính cung cấp khả năng giải thích dễ dàng hơn. Các mô hình phi tuyến tính khó giải thích nhưng có thể đưa ra dự đoán chính xác hơn.
Dưới đây là danh sách các thuật toán học có giám sát được sử dụng phổ biến nhất:
- Hồi quy tuyến tính
- Hồi quy logistic
- Phân tích tuyến tính
- Phân tích bậc hai
- Cây quyết định
- Naive bayes
- Hỗ trợ máy vector
- Mạng nơron
Thuật toán học không giám sát
Một thuật toán học tập không giám sát có thể được sử dụng khi chúng ta có danh sách các biến (X 1 , X 2 , X 3 ,…, X p ) và chúng ta muốn tìm cấu trúc hoặc mẫu cơ bản trong dữ liệu.
Có hai loại thuật toán học không giám sát chính:
1. Phân cụm: Sử dụng các loại thuật toán này, chúng ta cố gắng tìm "các cụm" quan sát trong tập dữ liệu tương tự với nhau. Điều này thường được sử dụng, ví dụ trong bài toán bán hàng, khi một công ty muốn xác định các nhóm khách hàng có thói quen mua sắm giống nhau để họ có thể tạo ra các chiến lược tiếp thị cụ thể nhằm vào các nhóm khách hàng nhất định.
2. Kết hợp: Sử dụng các loại thuật toán này, chúng ta cố gắng tìm "các quy tắc" có thể được sử dụng để minh hoạ các liên kết. Ví dụ: các nhà bán lẻ có thể phát triển một thuật toán liên kết cho biết “nếu một khách hàng mua sản phẩm X thì rất có khả năng họ cũng mua sản phẩm Y.”
Dưới đây là danh sách các thuật toán học không giám sát được sử dụng phổ biến nhất:
- Principal component analysis
- K-means clustering
- K-medoids clustering
- Hierarchical clustering
- Apriori algorithm
------------------------------------------------------------
Bài 2: Hồi quy và phân lớp
Thuật toán học có giám sát có thể được phân loại thêm thành hai loại:
1. Hồi quy: (Biến phản hồi là liên tục)
Ví dụ: biến phản hồi có thể là:
- Trọng lượng
- Chiều cao
- Giá
- Thời gian
- Tổng số đơn vị
Giả sử chúng ta có tập dữ liệu chứa ba biến số của 100 ngôi nhà khác nhau: diện tích, số lượng phòng tắm và giá bán.
Có thể xây dựng mô hình hồi quy với diện tích và số lượng phòng tắm làm biến giải thích và giá bán làm biến phản hồi.
Với mô hình này có thể dự đoán giá bán của một ngôi nhà, dựa trên diện tích và số lượng phòng tắm của nó.
Đây là một ví dụ về mô hình hồi quy vì biến phản hồi (giá bán) là liên tục.
Cách phổ biến nhất để đo độ chính xác của mô hình hồi quy là sử dụng đại lượng RMSE, đây là đại lượng cho chúng ta biết trung bình các giá trị dự đoán sai khác thế nào so với các giá trị quan sát được trong một mô hình. RMSE được tính như sau:
RMSE = √ Σ (P i - O i ) 2 / n
ở đây:
- Σ là ký hiệu "tổng"
- Pi là giá trị dự đoán cho lần quan sát thứ i
- Oi là giá trị quan sát được cho lần quan sát thứ i
- n là kích thước mẫu
RMSE càng nhỏ, mô hình hồi quy càng tốt và phù hợp với dữ liệu.
2. Phân lớp: (Biến phản hồi có thể phân lớp).
Ví dụ: biến phản hồi có thể nhận các giá trị sau:
- Nam hay nữ
- Đạt hay không đạt
- Thấp, trung bình hoặc cao
Trong mỗi trường hợp, mô hình phân lớp tìm cách dự đoán một số nhãn của lớp.
Ví dụ về phân lớp:Giả sử chúng ta có một tập dữ liệu chứa ba biến số của 100 cầu thủ bóng rổ khác nhau: điểm trung bình mỗi trận, level của các cầu thủ và dự báo liệu họ có được dự giải NBA hay không.
Chúng ta có thể sử dụng mô hình phân lớp sử dụng điểm trung bình mỗi trận và level làm biến giải thích và dự báo liệu họ có thể chơi cho giải NBA làm biến phản hồi.
Sau đó, chúng ta sử dụng mô hình này để dự đoán liệu một cầu thủ nào đó có được đưa dự giải NBA hay không dựa trên điểm trung bình mỗi trận đấu và level của họ.
Đây là một ví dụ về mô hình phân lớp vì biến phản hồi (“dự báo liệu họ được hay không được chơi cho giải NBA”) là phân lớp. Nghĩa là, biến dự báo này chỉ có thể nhận các giá trị trong hai danh mục khác nhau: “Được hơi” hoặc “Không được chơi”.
Cách phổ biến nhất để đo độ chính xác của một mô hình phân lớp là chỉ cần tính toán tỷ lệ phần trăm các phân loại đúng mà mô hình tạo ra:
Accuracy = correction classifications / total attempted classifications * 100%
Độ chính xác = phân lớp hiệu chỉnh / tổng số phân lớp đã xem xét*100%
Ví dụ: Nếu mô hình xác định chính xác một cầu thủ có được đưa vào NBA 88 lần trong số 100 lần thì độ chính xác của mô hình là:
Độ chính xác = (88/100) * 100% = 88%
Độ chính xác càng cao, mô hình phân lớp càng có khả năng dự đoán kết quả tốt.
Điểm giống nhau giữa hồi quy và phân lớp
Các thuật toán hồi quy và phân lớp tương tự nhau ở một số điểm sau:
- Cả hai đều là các thuật toán học có giám sát, tức là cả hai đều liên quan đến một biến phản hồi.
- Cả hai đều sử dụng một hoặc nhiều biến giải thích để xây dựng mô hình nhằm dự đoán một số phản hồi.
- Cả hai đều có thể được sử dụng để hiểu những thay đổi giá trị của các biến giải thích ảnh hưởng đến giá trị của một biến phản hồi như thế nào.
Sự khác biệt giữa hồi quy và phân lớp
Thuật toán hồi quy và phân lớp khác nhau ở chỗ:
- Các thuật toán hồi quy tìm cách dự đoán một giá trị và các thuật toán phân lớp tìm cách dự đoán một nhãn lớp.
- Cách chúng ta đo lường độ chính xác của mô hình hồi quy và phân lớp khác nhau.
Chuyển đổi hồi quy thành phân lớp
Bài toán hồi quy có thể được chuyển đổi thành bài toán phân lớp bằng cách đơn giản là rời rạc hoá (discretizing) biến phản hồi.
Ví dụ: giả sử chúng ta có một tập dữ liệu chứa ba biến: diện tích, số lượng phòng tắm và giá bán.
Chúng ta có thể xây dựng mô hình hồi quy bằng cách sử dụng diện tích và số lượng phòng tắm để dự đoán giá bán.
Tuy nhiên, chúng ta có thể phân lớp giá bán thành ba loại khác nhau:
- $80k - $160k: “Giá bán thấp”
- $161k - $240k: “Giá bán trung bình”
- $241k - $320k: “Giá bán cao”
Sau đó, chúng ta có thể sử dụng diện tích và số lượng phòng tắm làm các biến giải thích để dự đoán lớp (thấp, trung bình hoặc cao) cho giá bán của ngôi nhà.
Đây chính là bài toán phân lớp, vì chúng ta đang cố gắng xếp mỗi ngôi nhà vào một lớp.



Nhận xét
Đăng nhận xét